Long Memory in Time Series PhD Course

Department of Mathematical Sciences, Aalborg University

Course Description

Motivation

Time series analysis looks to capture the intrinsic information contained in the data by the use of statistical models. The typical model used in time series is the autoregressive moving average, \(ARMA\), given by \[x_t = \alpha_0+\alpha_1x_{t-1}+\cdots+\alpha_px_{t-p}+\varepsilon_t+\theta_1\varepsilon_{t-1}+\cdots+\theta_q\varepsilon_{t-q},\] where \(\{\varepsilon_t\}\) is a random disturbance.

Long Memory deals with the notion that certain series have autocorrelation functions, a measure of the impact of past observations, that decay slower than what any \(ARMA\) model can account for. The autocorrelation function for a long memory process shows hyperbolic decay instead of the typical geometric decay for \(ARMA\) models. This translates into perturbations having significant effects even after much time has passed. Its presence has repercussions for inference and prediction.

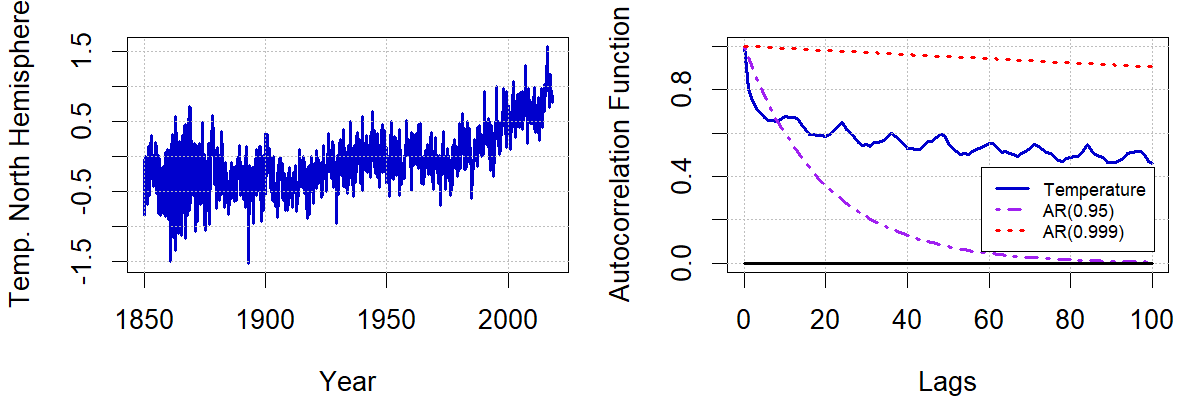
Long memory has been detected in several time series, including inflation, volatility measures, electricity prices, and temperature. As an example, Figure 1 presents the monthly temperature deviations series of the Northern Hemisphere and its autocorrelation function. The series presents long memory in the sense that its autocorrelation function is still significant after 100 periods. Any disturbance in temperature takes a long time to disappear, which is relevant for studies like the ones associated with Climate Change.

Figure 1: Temperature for Northern Hemisphere and its autocorrelation function.

This course introduces to models for time series with such strong persistence and tools for the statistical analysis thereof. The leading model is fractional integration of order \(d\), \(I(d)\). We discuss the properties of sample moments and conditions for limiting normality. Next, the estimation of the memory parameter \(d\) is addressed.

Then we turn to efficient tests for values of \(d\). Further, we will study regression analysis under fractional cointegration amongst several time series. Moreover, a competing model to fractional integration called harmonic weighting is introduced. If time allows, we may briefly touch upon further topics such as long memory in volatility, cyclical long memory or forecasting.

Background and Reading

  1. Our starting point is the short-memory \(I(0)\) process covered in classical books by , or . Relevant background material will be covered in quick review chapters in the beginning of this course.

  2. From \(I(0)\) we enter the range of stationary long memory, \(0 < d < 1/2\), continue with (different degrees of) nonstationarity and move towards unit roots, \(I(1)\).

  3. Long memory has received a lot of attention in time series analysis over the last decades. For instance, the updated edition by Box et al. (2015) contains a section on long memory and fractional integration, and so does Palma (2016); earlier textbooks like Brockwell and Davis (1991, Sect. 13.2), and Fuller (1996, Sect. 2.11) include short sections on this topic, too.

  4. Much of the material treated in this course is covered in the books by Beran et al. (2013), Giraitis, Koul, and Surgailis (2012), or Hassler (2019). We will walk through an extensive set of slides with many details.

  5. The structure of this course, most of the material and the notation from the slides are taken from Hassler (2019).

Contents

  1. Empirical Examples
  2. Review: Stationary Processes
  3. Review: Moving Averages
  4. Frequency Domain
  5. Differencing and Integration
  6. Fractionally Integrated Processes, \(I(d)\)
  7. Sample Mean
  8. Estimation of \(d\) and Inference
  9. Harmonically Weighted Processes
  10. Testing
  11. Fractional Cointegration
  12. Further Topics

Instructor

Prof. Dr. Uwe Hassler from Goethe University Frankfurt.

Reading Material

Beran, J., Y. Feng, S. Ghosh, and R. Kulik. 2013. Long-Memory Processes: Probabilistic Properties and Statistical Methods. Springer.
Box, G. E. P., G. M. Jenkins, G. C. Reinsel, and G. M. Ljung. 2015. Time Series Analysis: Forecasting and Control. 5th ed. Wiley.
Brockwell, P. J., and R. A. Davis. 1991. Time Series: Theory and Methods. 2nd ed. Springer.
Fuller, W. A. 1996. Introduction to Statistical Time Series. 2nd ed. Wiley.
Giraitis, L., H. L. Koul, and D. Surgailis. 2012. Large Sample Inference for Long Memory Processes. Imperial College Press.
Hamilton, J. D. 1994. Time Series Analysis. Princeton University Press.
Hassler, U. 2019. Time Series Analysis with Long Memory in View. Wiley.
Palma, W. 2016. Time Series Analysis. Wiley.

Schedule

The course will be held on November 26th-27th, 2024. The schedule is as follows:

Day 1

  • Registration with Coffee: 10:00-10:30 at the Department of Mathematical Sciences, Aalborg University.

  • Morning: Lectures from 10:30-12:00.

  • Lunch: 12:00-13:00 at Innovate (across the street from the Department of Mathematical Sciences).

  • Afternoon: Lectures from 13:00-14:30 and from 15:00-16:30. Coffee break will be held at 14:30.

  • Dinner: 18:00 at Wildebeest, Østerbro 12, 9000 Aalborg.

Day 2

  • Coffee: 10:00-10:30 at the Department of Mathematical Sciences, Aalborg University.

  • Morning: Lectures from 10:30-12:00.

  • Lunch: 12:00-13:00 at Innovate (across the street from the Department of Mathematical Sciences).

  • Afternoon: Lectures from 13:00-14:30 and from 15:00-16:30. Coffee break will be held at 14:30.

  • Course ends: 16:30.

Prerequisites

Basic knowledge of time series and statistics.

Logistics

Venue

The course will be held at the Department of Mathematical Sciences, Aalborg University, Aalborg, Denmark.

The Department of Mathematical Sciences is located at Thomas Manns Vej 23, 9220 Aalborg East, Denmark.

Fee

The course is free of charge for the students from AAU, AU, KU, CBS and SDU. Questions about cost for students from other universities should be directed to J. Eduardo Vera-Valdés.

Lunch, coffee breaks, and course dinner are included, provided by the Danish Graduate Programme in Economics (DGPE).

Costs associated with transportation and accommodation should be covered by the participants’ home institutions.

ECTS Credits

Upon completing all course activities, participants will be awarded 3 ECTS credits and a course certificate.

Registration

Register by filling out this form.

Deadline for registration is November 21st, 2024.

Connection to AWE VI Long Memory Symposium in Aarhus University

Participants in the course are encouraged to attend the AWE VI Long Memory Symposium in Aarhus University on November 28th-29th, 2024.

The symposium will feature presentations on long memory in time series and related topics. Participation in the symposium is free of charge, but registration is required.

More information about the symposium will be available soon.

Questions

For any questions regarding the course, please contact J. Eduardo Vera-Valdés, eduardo@math.aau.dk.

We look forward to welcoming you to Denmark in November!